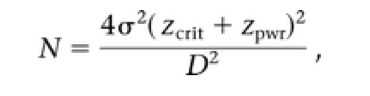Beta-alanine revisited: Failing to plan, or planning to fail?

In the past 2.5 years, a few more studies on beta-alanine have emerged. As I’ve written before, my goal isn’t to become the anti-beta-alanine blogger, but I do feel that watching this supplement develop from its relative inception to its current state does provide an interesting prototype for how similar products develop a strong following despite the limitations on the research available to support (or not support) its use.

Surprisingly, beta-alanine has not panned out to be as effective as previously touted. One study on the effect of beta-alanine supplementation on endurance performance and body composition in men doing HIIT failed to detect a difference BETWEEN placebo and beta-alanine in terms of VO2-peak, time to exhaustion, or body composition, despite finding statistically significant differences WITHIN groups (i.e. the beta-alanine group did better compared to itself at baseline, but on average, no better than the placebo group).

However, the prevailing limitation to these studies, ultimately comes down to sample size, and as a result of what I’m going to talk about in this post, whether the study that would be required to demonstrate an effect for beta-alanine on the variable of your choice, AND that would show that the difference observed between a beta-alanine group and a placebo group was VERY likely not an effect observed by chance alone would ever be possible or even worth doing.

The p-value is a number. That’s it. It is mathematically calculated. The calculation may be a little complicated, but it is still a calculated number. So, yes, a p-value can be manipulated, insofar as one can optimize the factors that affect the p-value. You can, of course, OVER-optimize for a significant p-value, but that’s usually pretty expensive, and the supplement companies would have us believe that it’s too expensive to run an optimized study, so there’s very little danger that someone is going to out of their way to fund an OVER-optimized one.

The equation that is used to compare two averages or means to each other looks like this:

N is the total sample size (the total of both groups together). The weird “o” with the squiggly tail is a small case sigma, and represents the variance of the sample (in this case, a standard deviation). D represents the mean difference observed between the two comparison groups. Zcrit is the Z-score for the critical p-value at which one would conclude that the effect observed is not by chance alone; Zpwr is the Z-score for the probability that one would fail to detect a difference between the two samples incorrectly, and is related to power (for those of you who care, but it’s not actually very relevant to the point I want to make).

Zcrit and Zpwr are two variables that most researcher rarely touch. There are reasons to mess with them, but on the whole, Zcrit will be 1.96 (the Z-score for a p-value of 0.05) and Zpwr will be 0.842 (the Z-score that corresponds to 80% power).

The number 4 is just the number 4.

So, ultimately, the only two things that ACTUALLY vary when it comes to calculating a sample size is sigma and D.

Some of you might ask at this point, “Well, aren’t you most interested in the power of a study that employs a small sample size?”

I’m of the opinion that my brain is actually quite lazy (read: I am lazy.) And while the higher functioning parts of my brain COULD deal with interpreting a power number, I feel that the effect of spitting out a power calculation is actually quite thinking-intensive and doesn’t quite capture the appropriate sentiment of exactly how harmful a small, underpowered study actually is.

Enough of this geek-speak, let’s plug in some numbers, shall we?

In one of the more recent beta-alanine trials (a randomized controlled trial of 46 college aged men; that’s 23 per group), time to exhaustion in the beta-alanine group at baseline was 1168.2 seconds (SD 163.6) and in the placebo group at baseline, 1128.7 seconds (SD 166.9). After 28 days of beta-alanine or nothing (and HIIT), time to exhaustion in the beta-alanine group was 1386.7 seconds (SD 234.9) and in the placebo group 1299.6 seconds (SD 164.9).

At a glance, the beta-alanine group fared better. They started out marginally better than the placebo group as a whole (about 40 seconds better), and ended, on average, about 87 seconds better than the placebo group. However, while the average time to exhaustion was better, it seems that the consistently in the result got worse, as reflected by the increase in the variance (or spread) of time to exhaustion values in the beta-alanine group. Eight-six seconds can mean the difference between gold and silver. But, in recreationally active men, 87 seconds probably doesn’t mean a whole lot. It probably means even less if you’re the guy on the lower end of that variance, because it means you might have done WORSE than when you started.

But, for argument’s sake, let’s say 87 seconds is REALLY important. And let’s give beta-alanine users the benefit of the doubt, since we can only use one variance number for this equation. We’ll fudge it so that as a group, they were just as consistent as the placebo group with a standard deviation of 164.9.

So, according to the sample size equation (the “^2” means squared, ’cause I have no idea how to superscript something in this blog editor):

N= 4(1.96+0.842)^2(164.9)(164.9) / (87.1)(87.1)

N= 112 (rounded to the nearest even number)

That means to demonstrate an 87 second difference between the two groups, with a standard deviation of 164.9 seconds, you would need 56 men per group; or slightly more than twice as many men as were actually used in that study.

But how many of you care about time to exhaustion? You just want to look good! In the same study, the average percent body fat in the beta-alanine group was 13.7% (SD 6.3) and in the placebo group, 16.1% (SD 7.5). After 28 days of supplementation of beta-alanine or placebo, the beta-alanine group had an average of 13.7% body fat (SD 5.6) and the placebo group had an average of 16.0% body fat (SD 7.9). That’s a mean difference between groups of 2.3%. Again, we will use the more advantageous standard deviation (5.6). Never mind the fact that body fat percentage didn’t actually change at all from pre to post-testing in the beta-alanine group itself; let’s say a difference of 2.3% body fat (which you would theoretically benefit from being on beta-alanine) is practically, somehow important.

N= 4(1.96+0.842)^2(5.6)(5.6) / (2.3)(2.3)

N= 186 (rounded to the nearest even number)

That means to demonstrate a 2.3% difference in body fat with a standard deviation of 5.6%, you would need 93 men in each group to calculate a p-value that would indicate that the 2.3% wasn’t a number obtained by chance alone. That’s roughly four time the number of subjects used in this study.

So what does all of this mean?

Well, there are two issues at play here. The first issue requires that you understand something about your body and what you want out of a supplement. If increasing your time to exhaustion by 87 seconds, plus or minus 164 seconds above and beyond what you could normally do with no beta-alanine (and yes, that means you COULD get slower–well, actually it means the data is probably not normally distributed, but for the sake of argument, let’s put that aside for now), is REALLY important to you, then it MIGHT be worth taking beta-alanine.

However…

If the difference we’re seeing in these studies between placebo and beta-alanine groups IS REALLY important, these trials are being set up to fail. Why? Because they’re inadequately powered. To answer the question, “Does beta-alanine increase time to exhaustion by 87 seconds plus or minus 164 seconds more than a placebo?”, the study would require a MINIMUM of 112 subjects.

The existing studies are destined to fail, unless the difference between groups is huge (i.e. way larger than 87 seconds), or the variance is very low(i.e. lower than 164 seconds). It is therefore impossible, with the current designs, to determine whether the effects observed in the beta-alanine groups are due to beta-alanine or freak chance. It is mathematically impossible for the equation, under the current parameters, to give us any information to guide our decisions about whether beta-alanine works or not!

And if the differences we’re seeing between placebo and beta-alanine groups AREN’T important (i.e. if I’m taking a supplement to improve my body-fat, it had better reduce my body fat by more than 0.1 percent (Seriously, is that even real, or just within the error of measurement?), then there’s no study of any size, significant p-value or not, that would indicate to me that the supplement is worth taking.

Bottom line: If the differences we’re seeing in these beta-alanine studies ARE practically important, then until there are studies with 186 people in them, the question of whether beta-alanine works under minimally-biased conditions will remain unanswered. And perhaps that’s where the companies want the answer to be–unanswered; so that you will continue to rely on anecdotal evidence to make your decisions. My opinion is that none of the differences between placebo (which IS different than taking nothing at all) and beta-alanine are important enough to warrant larger studies. It just doesn’t seem to have the effects that everyone is purporting it to have (and yes, this is despite there being very good physiological evidence that it does increase intramuscular carnosine, but the increase doesn’t seem to translate to anything useful).

The EBF point of view: Remember, that fitness decision making has three main components. Personal preference can and does at times, overrule all other things. But let’s not pretend the decisions made on personal experience are based on some “scientific” evidence. It’s been 2 years since my last beta-alanine post, and we are no further ahead now than we were back then.

References:

1. Smith AE, Waler AA, Graef JL et al. Effects of beta-alanine supplementation and high-intensity interval training on endurance performance and body composition in men; a double-blind trial. Journal of the International Society of Sports Nutrition 6(5), 2009.