The BMI: Lack of basic epidemiology knowledge makes us all dumber
This graph bothers me. The article from the New York Times bothers me more. For a long time I couldn’t figure out why. I’ve given talks on BMI, the history of the BMI and my practice of plastic surgery is permeated by the BMI. My opinion of the BMI has swung to both extremes—as a measurement that is junk, to a useful epidemiological tool, but not as a personal measurement, and now to something different entirely. I realized this because the graph bothered me; and the reason why it bothers me is because there is a fundamental construct problem with how the BMI is perceived; and when I say BMI, I mean the BMI cut-offs, because really, there is nothing wrong with dividing weights and heights.
The lay-press on the BMI is flawed because the people who do the reporting lack fundamental epidemiological basics; or, if they have the basics, they’re not using them, or, aren’t factoring them into the reporting.
Constructs
It’s been almost 2 decades since I took the most important course in my university career, “PHIL401: Medical Epistemology” If you’re a generator of knowledge, you cannot ignore the study of how knowledge is gained—how we come to know what we know. To do so is to turn a blind eye to the limits of the very knowledge you produce. Flipping the philosophy switch on allows one to see (still through an imperfect lens) issues that you can’t see when you’re sitting in the middle of the science issue. And while I could write about medical epistemology, you don’t have that much time on my blog to read about it.
Suffice it to say that it is useful, more often than not, to see disease as a construct, as opposed to an objective truth. That is, disease is not a fixed reality that exists outside of social perception and that disease is not just defined by the biological processes that are elucidated. The biology of disease is one component of the disease construct, but the construct includes many other components that are fundamental to its definition, including our collective feelings about it, and the kinds of people who are affected by the biological process. It is, by definition, a fluid construct, with the ability to change both in predictable and unpredictable ways.
So what, exactly, is the BMI construct?
The Body Mass Index is a unit-less number that you get when you divide a person’s weight in kilograms by the square of their height in meters (technically, it’s not unit-less, since it’s kilograms per square meter, but interpretively, it’s unit-less because it is exceedingly difficult to conceptualize what that actually means.) It is, essentially a way to compare a person’s weight to another person’s weight after adjusting for their height. This makes sense, because comparing the raw weight of a 6’4” person to a 5’6” person makes for difficult conversations when you’re trying to determine who’s obese (“X weighs 180lbs!” “J also weighs 180lbs!” “How can only one of them look obese?” See?)
However, the Index is not the construct. The construct is obesity, and its definition, which uses the BMI to quantify a number and whether that number lies above or below a cut-off (which is modifiable, for instance, by racial background.) For most populations, the definition of “overweight” is a BMI above 25, but below 30. “Obese” constructed as a BMI of over 30 (whether or not a “morbid” category is really needed is debatable.)
This definition is the central part of the obesity construct. With firm cut-offs, you are either overweight/obese or you are not. Similar problems arise with other firm diagnostic criteria (e.g. prior to DSM V, you could not have a diagnosis of anorexia nervosa until you had a BMI of less than 17.) By definition, no matter how much body fat you have, you cannot be defined as ‘overweight’ until your BMI is greater than 24.9, hence the term, “skinny fat”. And conversely, you cannot be classified as ‘not-overweight’ if your BMI IS over 25 (or the so-called “health obese”.)
The problem with language
If you look at many cases of different disease constructs, you will find that language is a huge issue. For instance, the “Spanish flu” in 1918, responsible for thousands of worldwide deaths, originated in France. The naming of a construct creates language that affects the rest of the construct—whether it be informative (creating the myth that the Spanish flu came from Spain), or affective (Gay-Related Immune Deficiency as an early name for HIV/AIDS.)
The word “obesity” is a completely loaded word. It carries connotation of all sorts of undesirable in its role as a synonym for “fat”. It is unfortunate, that those people whose BMI falls above 25 are labelled in the “overweight/obese” category because now we have a language problem.
The healthcare role of the BMI is to identify individuals who are at risk of either premature death or preventable disease (i.e. the so-called lifestyle modifiable diseases), or possibly preventable events (e.g. early knee replacement implant failure). Do you know what it’s not for? Singling out fat people. The problem with language, however, is that “obesity” is both a synonym that is use for politely referring to the word “fat”, and also a medical/scientific term that is NOT supposed to be laden with values. But NOW, the two have become irreversibly tangled such that no matter how much fat you’re carrying, if your BMI is higher than 25, you’re the synonym for “fat”’ and indirectly the synonym for “unhealthy” and “bad”.
This does not sit well with people who are, or appear, “under fat”. More about this later.
However, it’s no news to anyone that BMI is not a direct measure of fatness, because it doesn’t actually measure fat. It measures weight. And height. And study after study have called into question the utility of the BMI to accurately predict fatness to the point where a new “fat mass index” is now being proposed. And if BMI cutoffs can’t predict fatness, then why are we alarming all of these underfat people? (To be honest, I think it’s a bigger problem that the skinny fat folks might be lulled into a false sense of security, but that’s just me.)
I think the larger problem is that we have gone from identifying people who might be a higher risk, to calling people fat when we are not measuring fat. This creates a cognitive dissonance (“How can I be fat if I’m not fat?”) that muddies the waters substantially. We have gone from interpreting BMI as a proxy for fatness to interpreting it AS fatness by calling the cutoffs “obese”. This is the same problem that would arise if we confused an abnormal ECG reading with an actual heart attack and tried to use white-out to fix the heart attack. Sounds dumb, doesn’t it? That’s because it is.
The problem with the New York Times
If BMI is not a direct measure of adiposity, then it is, at most, a proxy for adiposity—that is, something that is highly related to adiposity, but imperfectly reflects it. The reason for its existence is because adiposity is so hard to measure directly (even the new FMI, or Fat-Mass Index is going to have problems when not measured by DEXA, which is STILL an indirect measurement.) So, by definition, it is a measurement that has error. The cutoffs for classifying individuals as obese or not-obese, therefore, are no different than any other diagnostic test; and that is how it should be treated.
Anyone who has taken any kind of epidemiology will know now where this is going. Anyone who doesn’t know where this is going had better not have been writing for the New York Times on “stuff that involves epidemiology.”
Oh wait. That already happened.
So, now, in this discussion, we have a construct (obesity) and a test for obesity (the BMI cutoffs). We acknowledge that the test for obesity is not the same as the construct itself, but an imperfect measurement. So how do we manage diagnostic tests? How can we tell if a test is worth using?
One way of NOT doing it is adding the false positives and false negatives and saying, “The test is wrong 18% of the time.”
Oh wait. That also already happened.
The statistics of diagnostic tests
This is a subject that has been hashed and re-hashed in the academic world. The standard answer is “sensitivity” and “specificity”, but I disagree in this particular case. But first, definitions:
Sensitivity is the proportion of people that a diagnostic test measures positive when we know that they have the disease. In this example, it is the proportion of people who meet the BMI cutoff of 25 when we know that their body fat is greater than 25% in men, or 35% in women. Note that since the body-fat cutoffs are different for men and women, you should probably generate separate statistics for each sex (I think it’s sex in the NHANES as opposed to gender.) We get this number from taking the number of people who have a BMI > 25 and dividing it by all of the people who have the disease (which include both people who have a BMI>25 AND the number of people who had a BMI<25, who had high body fat.)
If a test has high sensitivity, it means that it tests positive when the disease is present more often than testing negative when the disease is present. A test that is 100% sensitive means that it never tests negative if the disease is present. In the case of obesity, it would mean that no one would have a BMI<25 if their body fat was high, ie. there would be no one in the “skinny fat” category.
Specificity is the proportion of people that a diagnostic test measure negative when we know that they do not have the disease. In this example, it is proportion of people who do not meet the BMI cutoff of 25 when we know their body fat is less than 25% in men, or 35% in women. We get this number by taken the number of people who have a BMI<25 who don’t have high body fat and divide it by all the people who don’t have high body fat (which includes both people who have a BMI<25 AND people who have a BMI>25, who don’t have high body fat)
If a test has high specificity, it means that it tests negative when the disease is not present more often than testing positive when the disease is not present. A test that is 100% specific means that it never tests positive if the disease is not present. In the case of obesity, it would mean that no one would have a BMI>25 if their body fat was low, ie. there would be no one in the “healthy obese” category.
Looking at the NHANES 2006 data for men, the sensitivity for BMI cutoff test for high vs low body fat is 60/(60+6)=0.91 or 91%. The specificity is 22/(22+12)=0.65, or 65%.
Let’s interpret this.
The sensitivity is quite high. It means that if a man’s body fat is higher than 25%, that is will almost always result in a BMI >25. The specificity is not as promising. Sixty-five percent is closer to 50% than 100%. It means that if a man’s body fat is less than 25%, he will still most likely have a BMI<25, but that there are still quite a few men who will have a BMI>25 (false positives).
However, if you remember logic lessons, “All A is B” does not necessarily mean, “All B is A”.
If you are able to measure body fat, then using BMI is not useful because you already directly measured the variable of interest. BMI is only useful when you cannot measure body fat.
Sensitivity and specificity are fixed measurements for any given test and population because they are dependent on the reference standard—i.e. measuring when the disease is present before administering the test. However, what we tend to be interested in is whether a test can predict the presence of the disease. That is, can BMI be used to reliably say if a person has high body fat, as opposed to whether body fat can be used to say whether someone’s BMI will be higher or lower than 25.
This involves the ‘mirror’ measurements to sensitivity and specificity: positive and negative predictive value. These assume that the test result is known and the disease state is unknown.
With positive predictive value, we determine the proportion of people who when they test positive, actually have the disease. In the case of obesity, it’s the number of men who have a body fat >25% who have a BMI>25 divided by all the people who have a BMI>25 (which includes both those men who had a body fat greater or less than 25%.) A high positive predictive value means that the test correctly identifies “obese” people because there are only small number of people who had a a body fat<25% with a BMI greater than 25.
Negative predictive value is estimated by taking the number of men who had a body fat<25% who had a BMI<25 divided by all the men who had a BMI<25 (which includes both those men who had a body fat greater or less than 25%.) A high negative predictive value indicates that the test correctly identifies people with low body fat, since only a small number of people with low body fat would be able to have a high BMI and low body fat (false positives).
For predictive values, since the state of the disease is the unknown, they are affected by the prevalence of the disease. If a diagnostic test is poor at differentiating disease from not-disease (for example, it usually says, “yes” whether the disease is there or not) it can still have a high positive predictive value if the prevalence of the disease is high because the prevalence creates a situation in which the chances are high that ANY test, good or poor, will be “right”. Similarly, if a disease is quite rare, a poor test can still have a high negative predictive value because the test will be ‘right’ just by virtue of chance alone.
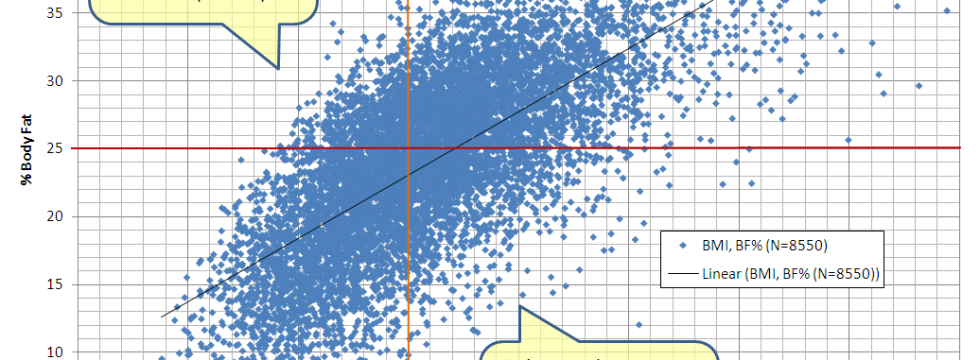
Since analysing the entire NHANES 2005-2006 dataset requires more time than a blog post would warrant, I took a subset of almost 1000 men (out of the roughly 2000-3000 who had DEXA data) to see why the seemingly simplistic graphic bothered me.
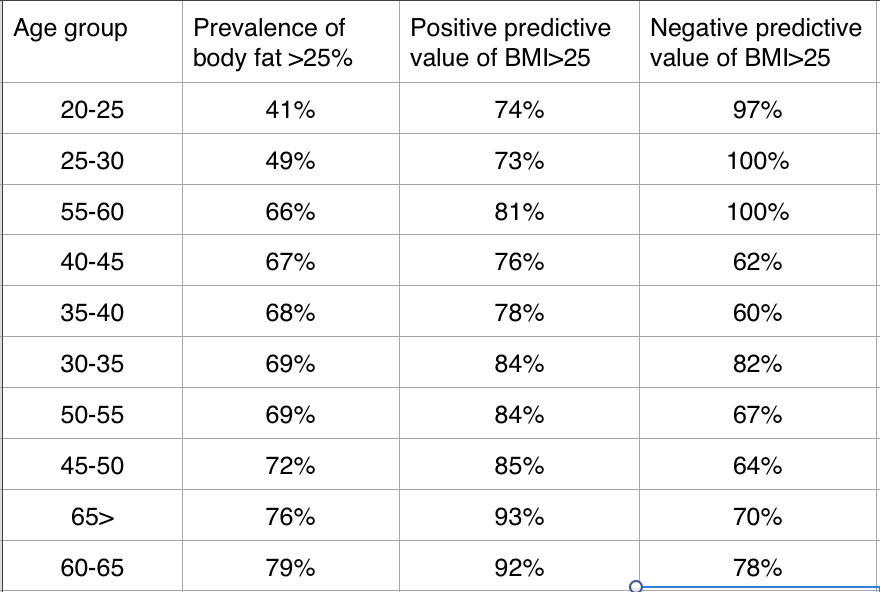
One thing that becomes glaringly clear, is the the prevalence of high body fat (defined, just a reminder as being greater than 25%) changes dramatically as the population ages. The sharpest contrast occurs in the age groups older than 30 year of age, where the lowest prevalence is at least a full 15% higher than men in their late 20’s.
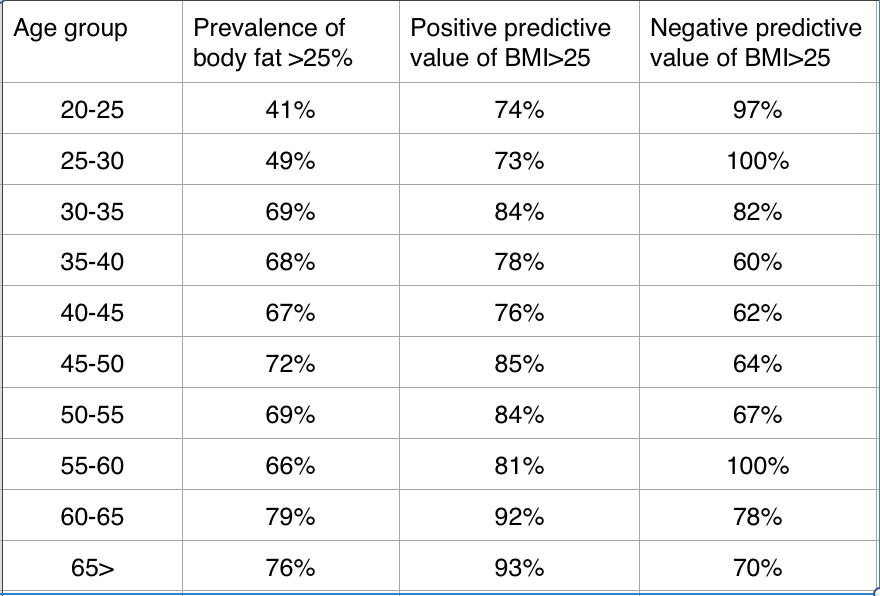
If we re-arrange the table in order of prevalence, the pattern between prevalence and positive predictive value becomes more apparent, and the age relationship appears to be possibly just a binary one.
That is to say that BMI has a fairly low positive predictive value for men in their 20’s, but after that, it gets better at predicting high body fat. To give you a frame of reference for positive predictive values, the positive predictive value of having a certain abnormality on an electrocardiogram (ST-segment elevation) in predicting a blockage in a coronary artery has been estimated to be around 85% (1). While the New York Times would have you believe that the BMI cut-offs are unreliable, it doesn’t appear to be the case when compared to other tests on which we rely to make critical health-care decisions.
Interestingly, the BMI cutoff of 25 seems to possibly have a bimodal distribution when ruling out high body fat—that is, in the age groups between 35 and 55 years of age, a BMI<25 might not be that good at indicating that your body fat is less than 25%, which is probably more concerning than a low positive predictive value since these individuals could be lulled into a false sense of security.
Diagnostic tests generally gear towards one side or the other—positive or negative predictive value. It is very difficult to produce a test that does well at identifying disease AND identifying its absence. For some diseases, having a test that can accurately say that a person doesn’t have the disease is more important than having one that says they DO have it, particularly in situations where positive diagnosis might be complicated. These tests prioritize maximizing the negative predictive value.
So with this information, I think that the role of BMI cutoffs favours identifying individuals at risk as opposed to identifying those individuals who are not at risk, since being at higher risk should trigger either more investigations, or possibly intervention (like weight loss).
Remember that the assumption of the obesity construct is that high body fat is potentially modifiable risk factor for bad things, and that in the current framework, BMI cutoffs are being used to identify people who are potentially at high body fat. The BMI cutoffs probably overestimate the number of people at risk of high body fat for men in their 20’s, but probably doesn’t overestimate things by that much for men over 30.
Remember also, that BMI is not a direct measurement of body fat. “Overestimated” Individuals who do not apparently have high body fat, but have a BMI higher than 25, can be further tested for body fat (e.g. DEXA scan) directly to rule in, or rule out obesity, if it’s that important of an issue.
The problem with the BMI, in my opinion, is really not in over-identifying people who are at risk, but under-identifying them, since having a BMI lower than 25, particularly for men over the age of 35, doesn’t trigger any health advice or extra testing to sort out those individuals who have normal BMI and normal to low body fat from those who have high body fat percentages.
However, having a high BMI, regardless of your body fat percentage, may still be a risk factor for bad things.
If we were to assume that BMI is not a measurement for body fat at all and that it should be thrown out as a measurement of body fat, this decision would still not negate reams of research that have been done on BMI as a risk factor for certain diseases. BMI DOES measure something. It is a measurement of mass, adjusted for height. We assume that the process by which certain diseases occurs is mediated through excess body fat. However, BMI has been shown to be an independent risk factor for some diseases such as osteoarthritis and cardiac issues. The papers use words like “obese” because that’s the word that is used to name the category defined as a BMI>29; but the word carries the wrong connotation of “excess body fat” (see the language problem?), since, as we have just shown and everyone is complaining about, there are individuals who do not have excess body fat who have more mass. Does that mean that lean individuals who have a higher BMI are safe because BMI might not be a great measure of excess body fat? What if there are health risks to simply having more mass, regardless of its composition?
Just because the association between BMI and body fat is not iron-clad (though it’s pretty close in age groups higher than 30, and definitely higher than 40) doesn’t mean that the risk factor isn’t there; it just might not be about the fat. What will be interesting to observe in the future is analyses where both BMI (or alternatively, fat-free mass) AND fat mass are accounted for. Being big and lean might not be all we think it’s cut out to be.
1. Zanuttini D, Armellini I, et al. Predictive value of electrocardiogram in diagnosing acute coronary artery lesions among patients with out-of-hospital-cardiac-arrast. Resuscitation 84(9):1250-1254, 2013.